Given:
The sequence is
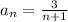
Required:
Find the first term, the second term, the third term, the fourth term and the 100th term.
Step-by-step explanation:
The given sequence is:
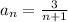
Substitute n = 1
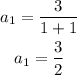
Substitute n = 2
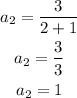
Substitute n = 3
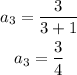
Substitute n = 4
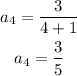
The term of the sequence are:
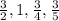
The given series is in HP
We will write it in AP as:
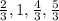
So the common difference of the given sequence is:
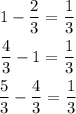
The nth term of the AP series is given by the formula:
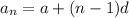
where a = first term
n = number of terms
d = common difference
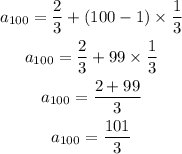
This is the 100th term for the AP.
The 100th term of the given HP sequence is:
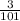
Final Answer:
