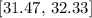Hello there. To solve this question, we have to remember some properties about confidence intervals.
To determine the confidence interval for a sample, given its mean and standard deviation, we use the formula:
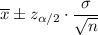
Whereas

The question gave:
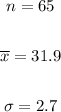
And we want a 80% confidence interval.
We determine the significance level using the formula:
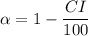
That is, the difference between the area from the confidence interval and the total area of the gaussian distribution:
Okay. In this case, we have that
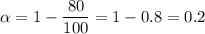
Therefore
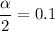
And we get that
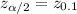
To determine this value, consider the table with Z-scores for a normal distribution that you can easily find on the internet.
In this case, we get
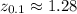
Such that the interval of confidence will be:
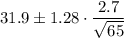
Using a calculator, we find that
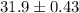
And the interval is: