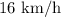Question

a motorboat takes 4 hours to travel 128 kilometers going up stream. the return trip takes 2 hours going downstream. what is the rate of the boat in still water and what is the rate of the current?

Answer 1

The rate of the boat in still water is;

`48\text{ km/h}`

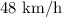
The rate of the current is;

`16\text{ km/h}`

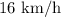
Step-by-step explanation:

Let x represent the rate of the boat in still water, and y represent the rate of the current;

Speed upstream is;

`x-y`

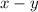
Speed downstream is;

`x+y`

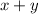
Recall that distance equals the product of speed and time;

Upstream the product is;

`4(x-y)=128------1`

Downstream;

`2(x+y)=128-------2`

Expand both equation and multiply equation 2 through by 2;

`\begin{gathered} 4x-4y=128--------1a \\ 2x+2y=128 \\ \text{ multiply through by 2;} \\ 4x+4y=256------2a \end{gathered}`

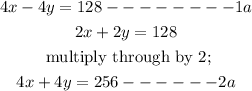
solve the simultaneous equation by elimination; add equation 1a and 2a together;

`\begin{gathered} 4x+4x+4y-4y=128+256 \\ 8x=384 \\ x=(384)/(8) \\ x=48 \end{gathered}`

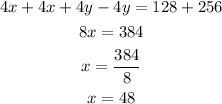
Then we can substitute x into equation equation 2 to get y;

`\begin{gathered} 2(x+y)=128 \\ x+y=(128)/(2) \\ y=64-x \\ y=64-48 \\ y=16 \end{gathered}`

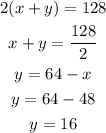
Therefore, the rate of the boat in still water is;

`48\text{ km/h}`

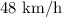
The rate of the current is;

`16\text{ km/h}`