Question

In Quinn's dormitory room, there are three snooze alarm clocks, each of which is set at a different time. Clock A goes off every 25 minutes, Clock B goes off every 60 minutes, and Clock C goes off every 100 minuets. If all three clocks go off at 6:00am, How long will it be before the clocks go off simultaneously again after 6:00am?

Answer 1

first, we find the L.C.M of 25mins for clock A, 60mins for clock B and 100mins for clock C.

The L.C.M of 25mimutes, 60minutes, and 100minutes for clock C is:

`300\text{minutes}`

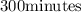
Then, we are going to convert the 300minutes to hours and add the result to 6:00am.

Thus, we have:

`300\text{minutes}=(300)/(60)=5\text{hours}`

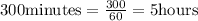
Adding the 5 hours to 6:00 am, the clocks go off simultaneously at:

`11\colon00am`

Hence, it takes the clocks 5hours before the clocks go off simultaneously again