Given a chess game has the following:
2 kings
2 queens
4 rooks
4 bishops
4 knights
16 pawns
One game piece is randomly selected, replaced, the another is chosen.
Total number of game piece = 2 + 2 + 4 + 4 + 4 + 16 = 32
To find the probability of selecting a king or queen, then pawn, first find the probability of selecting a king or queen, and the probability of selecting a pawn.
We have:
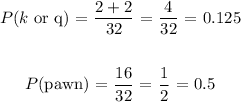
Now, let's P(king or queen) and P(pawn):

Therefore, the probability of selecting a king or queen, then a pawn is 0.0625
ANSWER:
0.0625