Question

Find the area of a triangle bounded by the y-axis, the line f(x)=9-\frac{6}{7}x, and the line perpendicular to f(x) that passes through the origin. Type your answer rounded to the nearest hundredth.The area is Answer square units.

Answer 1

To understand the question let us draw a figure

We need to find the area of triangle OAB

Its base is OA with a length of 9

Its height BC

We need to find BC

It is equal to the x-coordinate of point B

Then we have to solve the equations of the 2 perpendicular lines BA and BO to find the x coordinate of B

The equation of BA is given

`y=9-(6)/(7)x\rightarrow(1)`

Since the slope of perpendicular lines are opposite reciprocal of each other

Since the slope of line AB is -6/7, then the slope of OB is 7/6

Since the line OB passes through the origin, then its y-intercept = 0

Then the equation of BO is

`y=(7)/(6)x\rightarrow(2)`

Equate (1) and (2)

`(7)/(6)x=9-(6)/(7)x`

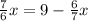
Add 6/7 x to both sides

`\begin{gathered} (7)/(6)x+(6)/(7)x=9-(6)/(7)x+(6)/(7)x \\ (85)/(42)x=9 \end{gathered}`

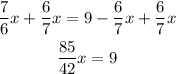
Divide both sides by 85/42

`x=(378)/(85)`

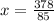
Then the height of the triangle is 378/85

Then the area of the triangle is

`\begin{gathered} A=(1)/(2)(9)((378)/(85)) \\ A=20.01176471 \end{gathered}`

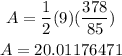
Then the area is 20.01 square units to the nearest hundredth