Question

A ball is thrown vertically upward from ground level at a rate of 140 feet per second.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given function

`\begin{gathered} h=-16t^2+v_0t+h_0-----equation\text{ 1} \\ where: \\ v_0\Rightarrow initial\text{ velocity of the stone} \\ h_0\Rightarrow initial\text{ height of the stone} \end{gathered}`

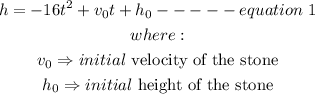
STEP 2: Find the maximum height

To calculate the maximum height and the time t it takes to reach this height, we take the derivative of h with respect to t as seen below:

`h^{^(\prime)}=(dh)/(dt)=-32t+v_0`

STEP 3: Determine the critical point of the function

At the critical point, h' equals zero, therefore,

`\begin{gathered} h^(\prime)=-32t+v_0 \\ where\text{ h'=0 at the critical point} \\ -32t+v_0=0 \\ where\text{ v0=140} \\ \therefore-32t+140=0 \\ Subtract\text{ 140 from both sides} \\ -32t+140-140=0-140 \\ -32t=-140 \\ t=(-140)/(-32) \\ t=4.375seconds \\ t\approx4.38\text{ seconds} \end{gathered}`

STEP 4: Determine the extreme point of the function

To determine the extreme point of the function, we take the second derivative of the function as seen below:

`\begin{gathered} h^(\prime)^(\prime)=(d^2h)/(dt^2)=-32 \\ where\text{ h''>0, we have a minimum point} \\ where\text{ h''<0, we have a maximum point.} \end{gathered}`

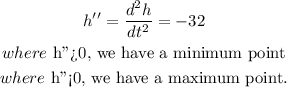
Since the second derivative obtained is negative, we have a maximum point.

Thus, the stone reaches maximum height after 4.38 seconds.

STEP 4: Evaluate the maximum height reached by the stone

By substituting the value, 4.375 in equation 1, we have:

`\begin{gathered} h=-16(4.375^2)+140(4.375)+0 \\ Ground\text{ level means that h =0} \\ h=-306.25+612.5=306.25 \\ h=306.25ft \end{gathered}`

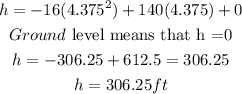
Hence, the stones reaches its maximum height after 4.38 seconds . The maximum height the stone reaches is 306.25 feet.