In the right triangle, there is a relation between the legs of the right angle and the hypotenuse

a and b are the legs of the right angle
c is the hypotenuse
Note that the hypotenuse is the longest side in the right triangle
Since the 3 sides are 6, 12, 13, then
6 and 12 are the legs of the right angle
13 is the hypotenuse
By using the relation above
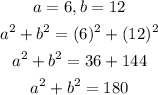
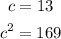
The values of them are not equal as the relation above

Then 6, 12, 13 can not form sides of a right triangle
We disagree
Because the sum of the squares of the smaller sides is not equal to the square of the longest side.