The general exponential regression equation is
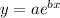
We get (0,847) and (1, 972) points from the table.
Substitute x=0 and y=847, we get
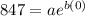
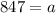
Substitute a=847 in the general equation, we get
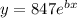
Substitute x=1 and y=972, we get
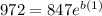
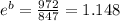
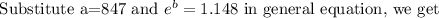
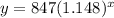
Hence the exponential regression equation is
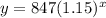
Substitute x=8 to find the number of bacteria after 8 hours.
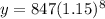
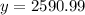
Round off,
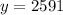
The number of bacteria after 8 hours is 2591 bacterias.