Question

You deposit $650 in an account paying 7.1% simple interest. Find the future value of the investment after 2 years. (Round your answer to two decimal places.)$

Answer 1

The given parameters in the question are

`\begin{gathered} Deposit=A=P.V=\text{ \$650} \\ \text{rate}=R=7.1\text{ \%} \\ \text{time =t=2 years} \end{gathered}`

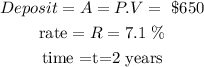
The formula to calculate the future value is given below as

`\begin{gathered} \text{future value=present value +simple interest} \\ F\mathrm{}V=P\mathrm{}V+I \end{gathered}`

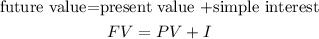
The formula for simple interest (I) is

`\text{Interest (I)=}\frac{\text{ P}* R* T}{100}`

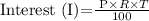
Substituting the values, we will have the interest to be

`\begin{gathered} I=(650*7.1*2)/(100) \\ I=(9230)/(100) \\ I=\text{ \$92.3} \end{gathered}`

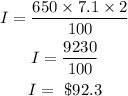
To calculate the future value,

`\begin{gathered} F\mathrm{}V=P\mathrm{}V+I \\ F\mathrm{}V=\text{ \$650 + \$92.3} \\ F\mathrm{}V=\text{ \$742.30} \end{gathered}`

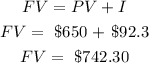
Hence,

The future value of the investment after two years will be = $742.30