Solution
For this case we can select two fractions less than 1, lets say:
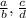
Where a
Then if we divide both fractions we have:
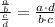
From this we can use the fact that this fraction is less than 1 but is also higher than the original fractions following the priciple that the smaller a number is, the more of them can “fit” (divided) into a number.