In order to better understand, let's draw the segment and both axis:
Then, let's calculate the slope of this segment, using the following formula for two points (x1, y1) and (x2, y2):

Using points A and B, we have:
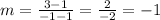
That means for every unitary increase in x, the value of y decreases by 1 unit.
So, from point (-1, 3), let's add 1 unit to x and decrease 1 unit from y, then we have point (0, 2).
We can see that both x and y coordinates of this new point are the average of A and B coordinates (0 is the average of -1 and 1, 2 is the average of 1 and 3).
Therefore the line segment AB is divided in a ratio of 1 to 1 (it is divided into two equal segments)