Question

Suppose that y varies inversely as the square of x, and that y = 3 when x = 18. What is y when x = 20? Round your answer to two decimal places if necessary.

Answer 1

If y varies inversely with square x, so

`\begin{gathered} y=(k)/(x^2) \\ OR \\ (y_1)/(y_2)=(x^2_2)/(x^2_1) \end{gathered}`

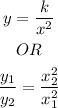
Where k is the constant of variation, you can get it by using the initial values of x and y

We will use the second rule

Since y is 3 when x is 18 (initial values), so

`\begin{gathered} y_1=3 \\ x_1=18 \end{gathered}`

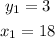
We need to find y when x is 20

`\begin{gathered} y_2=? \\ x_2=20 \end{gathered}`

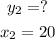
Let us substitute them in the second rule

`\begin{gathered} (3)/(y_2)=((20)^2)/((18)^2) \\ (3)/(y_2)=(400)/(324) \end{gathered}`

By using cross multiplication

`\begin{gathered} 400* y_2=3*324 \\ 400y_2=972 \end{gathered}`

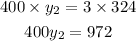
Divide both sides by 400

`\begin{gathered} (400y_2)/(400)=(972)/(400) \\ y_2=2.43 \end{gathered}`

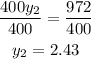
The value of y is 2.43 (There is no necessary to round it)

In direct proportion, if y increasing x also increasing (both increasing or decreasing)

In inverse proportion, if y increasing, x decreasing and vice versa