So in order to find the probability that the weight of a randomly selected steer is between 1169lbs and 1400lbs we first need to find the z values corresponding to 1169 and 1400. The z values are calculated by using the mean and the standard deviation of the population of steers:
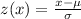
Where mu is the mean and sigma the standard deviation. Then we have:
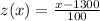
And the two z values that we need are:
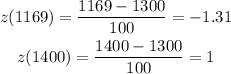
Then we look at a z value table and see the values corresponding to these two z values:
So the values given by the table are 0.0951 and 0.8413. This means that the probability that the weight of a randomly selected steer is between 1169lbs and 1400lbs is 0.8413-0.0951=0.7462. Then the answer is 0.7462.