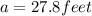Question

In this discussion, you will apply the Law of Sines to real-world examples.Write your own real-world problem to be solved using the Law-of Sines.1. Post your problem to the discussion board.

Answer 1

Example

You are standing 10 feet away from a certain leaning tower. Find the ladder length that is needed to reach the third floor of the leaning tower if the ladder is placed where you are standing. The angle that is formed by the tower and the ground is 108 degrees, and the angle formed by the tower at the third floor and the ladder will be 20 degrees.

Solution:

We begin by first drawing out our problem. We draw our triangle and label it with the information that is given.

Okay. We see that the side we want to find is the ladder side. We can arbitrarily label that with a. Because we are dealing with any kind of triangle, it doesn't matter which side we label with a, b, or c. If we label the ladder side as a, then our angle A is 108, the angle opposite our side a. We can go ahead and label the 10 as side b. Our angle B is then 20.

Looking at what we have now, we see that we only need the first two parts of our law of sines to find our answer:

The law of sines formula is,

`(a)/(sinA)=(b)/(sinB)`

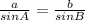
Plugging in our values,

`(a)/(sin108)=(10)/(sin20)`

Evaluate for a

`\begin{gathered} Cross\text{ multiply} \\ a=(10sin108)/(sin20)=27.80703\approx27.8(1\text{ decimal place\rparen} \\ \therefore27.80703 \end{gathered}`

Hence, the ladder length that is needed is

`a=27.8feet`