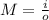Question

A lens magnifies an object by 6.1X. If the image is 3.33 m tall, how tall is the original object?

Answer 1

Let o be the size of the object. Since the lens magnifies the object by 6.1 and the image is 3.33 m tall, then:

`6.1* o=3.33m`

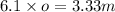
Divide both sides of the equation by 6.1 to find the value of o:

`\begin{gathered} (6.1* o)/(6.1)=(3.33m)/(6.1) \\ \Rightarrow o\approx0.546m \end{gathered}`

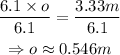
Therefore, the original object is 0.546m tall.

Remember the following definition for the magnification of an optical instrument:

`\text{magnification }=\frac{\text{image height}}{\text{ object height}}`

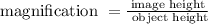
Which can also be written using M for magnification, i for image height and o for the object height:

`M=(i)/(o)`