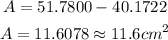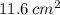
1) To find the shaded region, we need to find at first the area of the sector. And then subtract from that the area of that triangle.
2) Note that two legs of those three from that triangle are the radius of that circle. So let's begin by finding the area of the sector:

3) Now for the area of that triangle, we'll resort to one formula that relates to the sine of that angle since we don't know the measure of the height:
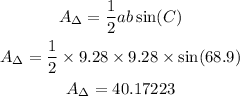
Note that we rounded off to the nearest hundredth
4) So now, we can subtract from the sector the area of that triangle: