SOLUTION
Since the circle is inscribe in the square, the lenght of the square will in turn be the diameter of the circle.
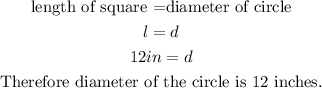
The area of a circle is calculated with the formula:
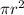

Substitute this value into the formula for area of a circle:
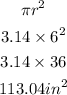
The area of the inscribed circle is 113.04 square inches.