According to special relativity, if an observer at rest measures a time interval Δt, then a clock traveling at speed v woud measure a time Δt' given by:
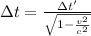
Notice that the denominator of the expression is always lower or equal to 1, which means that Δt (the time measured by a clock at rest) is greater than Δt'. This can be interpreted as if the moving clock was ticking slower than the clock at rest.
Isolate v from the expression:

Since 7 years elapses on Earth while only 1 hour elapses on the ship, then, replace Δt'=1h and Δt=7y, as well as c=3*10^8m/s:

Since the quotient (1h/61,362h)^2 is much smaller than 1, we can approximate the value of the square root as follows:
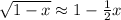
Then:
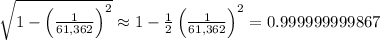
Then, the speed of the spaceship is:
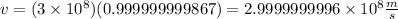
Therefore, the speed of the spaceship is 2.9999999996*10^8 meters per second, which is equivalent to 0.99999999987 times the speed of light.