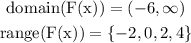Question

Find the domain and range in set notation; state if it is a function and a one to one function

Answer 1

Notice that this is a piecewise function, the solid dots mean 'including', and the open dots mean 'not including'. An example of a solid dot is the point (-3,-2), whereas an open dot is (-6,-2).

The first part of the function goes from (-6,-2) to (-3,-2) without including the first point. In other words,

`f_1(x)=-2,x\in(-6,-3\rbrack`

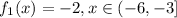
Similarly, the second part of the function goes from (-3,0) to (1,0), without including the first point. The function is

`f_2(x)=0,x\in(-3,1\rbrack`

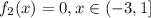
Repeat the process with the two remaining parts of the function and you will obtain:

`\begin{gathered} f_3(x)=2,x\in(1,4\rbrack \\ f_4(x)=4,x\in(4,\infty) \end{gathered}`

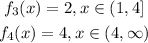
Therefore, the function in the image is

`F(x)=\begin{cases}-2,x\in(-6,-3\rbrack \\ 0,x\in(-3,1\rbrack \\ 2,x\in(1,4\rbrack \\ 4,x\in(4,\infty)\end{cases}`

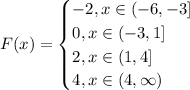
This is indeed a function (notice that the solid points coincide with the open points), and a one-to-one function.

Finally, we need to find its domain and range.

`\begin{gathered} \text{domain(F(x))}=(-6,\infty) \\ \text{range(F(x))}=\mleft\lbrace-2,0,2,4\mright\rbrace \end{gathered}`