SOLUTION
From the question given, to get how many inches of wooden stick that would be required to outline the perimeter of the banner, we have to find the perimeter of the triangle as shown below
So from above, perimeter is distance around a plane figure. So the perimeter of the triangle will be
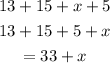
so, we need to find the value of x to get the perimeter
From the diagram above you can see that the triangle is made up of two right-triangles. For the smaller right angle triangle, the the hypotenuse is 13, so from Pythagoras, we have
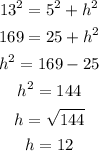
Now, h is for both the smaller and bigger right angle triangles. So for the bigger triangle, 15 is the hypotenuse. From Pythagoras, we have
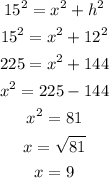
So, the perimeter becomes
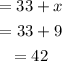
Hence the answer is 42 inches