We are given the following function:
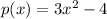
We are asked to determine the value of p(8a). That means that we will substitute the value of "x = 8a" in the function, like this:
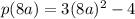
Now, we solve the exponents using the following property:
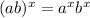
Applying the property we get:

Solving the products we get:
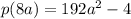
Since we can't simplify any further this is the final answer.