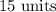Question

Point B is on line segment AC. Given AB = 3x, BC = 4x + 8, andAC = 5x + 10, determine the numerical length of AC.

Answer 1

The numerical length of AC is;

`15\text{ units}`

Step-by-step explanation:

Given that point B is on the line segment AC;

So,

`AC=AB+BC`

Given;

`\begin{gathered} AC=5x+10 \\ AB=3x \\ BC=4x+8 \end{gathered}`

substituting;

`\begin{gathered} AC=AB+BC \\ 5x+10=3x+4x+8 \\ 5x+10=7x+8 \end{gathered}`

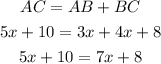
solving for x, we have;

`\begin{gathered} 5x+10=7x+8 \\ \text{subtract 8 from both sides;} \\ 5x+10-8=7x+8-8 \\ 5x+2=7x \\ \text{subtract 5x from both sides;} \\ 5x-5x+2=7x-5x \\ 2=2x \\ 2x=2 \\ \text{divide both sides by 2;} \\ (2x)/(2)=(2)/(2) \\ x=1 \end{gathered}`

Since we have derived the value of x, let us substitute the value of x to get AC;

`\begin{gathered} AC=5x+10 \\ AC=5(1)+10 \\ AC=15 \end{gathered}`

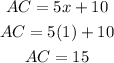
Therefore, the numerical length of AC is;

`15\text{ units}`