GIVEN:
We are given the set of functions as indicated in the attached image.
Required;
To determine which pair of functions are inverses of each other.
Step-by-step solution;
We shall solve each function one after the other to determine which pair are inverses of each other and which pair is not.
Option A:
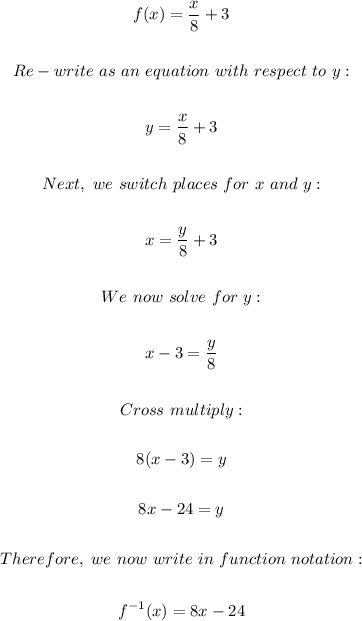
Therefore, option A is not a pair of inverse functions.
OptionB;

Therefore, option B is not a pair of inverse functions.
Option C:
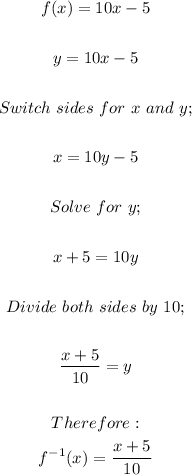
Therefore, option C is a pair of inverses.
Option D:
![\begin{gathered} f(x)=\sqrt[3]{6x} \\ \\ y=\sqrt[3]{6x} \\ \\ Switch\text{ }sides\text{ }for\text{ }x\text{ }and\text{ }y; \\ \\ x=\sqrt[3]{6y} \\ \\ Solve\text{ }for\text{ }y; \\ \\ Cube\text{ }both\text{ }sides; \\ \\ x^3=(\sqrt[3]{6y})^3 \\ \\ The\text{ }exponent\text{ }cancels\text{ }out\text{ }the\text{ }radical\text{ }on\text{ }the\text{ }right\text{ }side; \\ \\ x^3=6y \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }6; \\ \\ (x^3)/(6)=y \\ \\ Therefore: \\ \\ f^(-1)(x)=(x^3)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m9bmrofwcq7287ckcij92lh3ozwrpohm98.png)
Therefore, option D is not a pair of inverses.
ANSWER:
The pair of functions in option C are inverses of each other.