Question

Exercises 1-8, find the area of the shaded region. The radius of each circle is r. If twocircles are shown, r is the radius of the smaller circle and R is the radius of the largercircle.

Answer 1

0.67 cm^2

Step-by-step explanation:

The angle subtended by the shaded region is 360 - 240 = 120 degrees.

Therefore, the shaded region represents

`(120)/(360)=(1)/(3)`

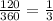
of the whole circle.

Now, the area of the whole circle is

`A=\pi r^2`

In our case, the radius is 0.8 cm; therefore,

`A=\pi*(0.8)^2`
`A=0.64\pi`
`\Rightarrow A=2.012`

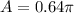
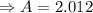
The area of the shaded portion is 1/3 of the area of the whole circle. Therefore,

`A_{\text{shaded}}=(1)/(3)*2.012`
`\boxed{A_{\text{shaded}}=0.67\; cm^2\text{.}}`

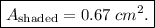
Hence, the area of the shaded portion is sqaure centimetres.