Answer:
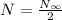
Vertex: (150, 17.33)
Explanation:
The equation for the parabola is given as:

Part 6
The x-coordinate of the vertex of the parabola is the equation of the axis of symmetry.
We can find the equation of the axis of symmetry using the formula:
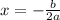
From the equation for K:
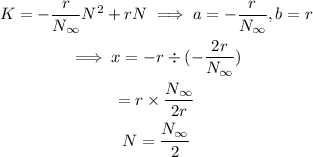
The equation of the x-coordinate of the vertex of the daily vs total cases parabola is:
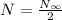
Part 7
• From part (4), the growth rate, r= ln(2)/3.
,
• Given that N∞ = 300 million
The coordinates of the vertex will be:
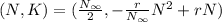
Replace N in the y-coordinate with the equation obtained from part(6).
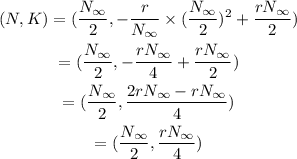
Substitute the given values:
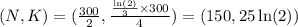
The coordinates of the vertex will be (150, 17.33).