Question

The length of a rectangle is two feet more than five times the width. The perimeter is 52 feet. Find the dimensions of the rectangle.

Answer 1

Let the length of the rectangle be L, the width be w and the perimeter P

The length of a rectangle is two feet more than five times the width, this means

`\begin{gathered} L=2+(5* w) \\ L=2+5w \\ P=52 \end{gathered}`

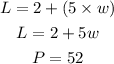
Also perimeter P of a rectangle is given as

`P=2(L+w)`

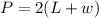
This becomes

`\begin{gathered} P=2(L+w) \\ 52=2(L+w) \\ 52=2L+2w \\ \text{Now }L=2+5w \\ \text{substituting we have } \end{gathered}`

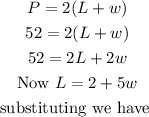
That

`\begin{gathered} 52=2L+2w \\ 52=2(2+5w)+2w \\ 52=4+10w+2w \\ \text{collecting like terms } \\ 52-4=10w+2w \\ 48=12w \\ w=(48)/(12) \\ w=4 \end{gathered}`

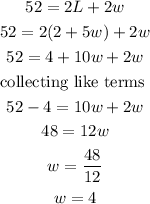
Hence the width is 4

The length becomes

`\begin{gathered} L=2+5w \\ L=2+5*4 \\ L=2+20 \\ L=22 \end{gathered}`

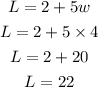
And the length is 22

Hence the dimensions of the rectangle is 22 by 4