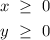Question

The Shredder, Inc. produces two types of paper shredders, home and office. The office model requires 3 hours to assembly and 12 finishing work units for finishing work, the home model requires 2 hours to assemble and 10 finishing work units for finishing. The maximum number of assembly hours available is 48 per day, and the maximum number of finishing hours available is 210 per day.Let x = the number of office model shredders produced per day and y = the number of home model shredders produced per day.Write the system of inequalities that represents the maximum number of shredders that can be produced in one day.NOTE: 4 inequalities are expected.

Answer 1

The inequalities are:

`\begin{gathered} x\ge\text{ 0} \\ y\text{ }\ge\text{ 0} \\ 3x\text{ + 2y}\leq\text{ 48} \\ 12x\text{ + 10y }\leq\text{ 210} \end{gathered}`

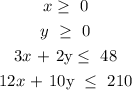
Step-by-step explanation:

Here, we want to write the system of inequalities that could represent the maximum number of shredders produced

From the question:

The office model requires 3 hours of assembly and 12 finishing work units

The home model requires 2 hours of assembly and 10 finishing work units

The maximum number of assembly hours per day is 48 hours

To write the equations, we multiply the number of possible shredders by the number of possible hours, then sum up the values to get the possible total hours

Thus:

`3x\text{ + 2y }\leq\text{ 48}`

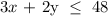
For the finishing hours, we have it that:

`12x\text{ + 10y }\leq\text{ 210}`

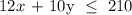
Also, we know that the numbers of shredders cannot be negative

Thus:

`\begin{gathered} x\text{ }\ge\text{ 0} \\ y\text{ }\ge\text{ 0} \end{gathered}`