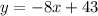If we have an equation of the form

then the equation of the perpendicular line is given by
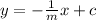
Now, keeping that in mind, the equation of the perpendicular line to y =-8x+7 is
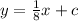
We find c by using the fact that this perpendicular line passes through (-6, -5)
Putting in x = -6 and y = -5 gives
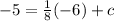
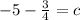
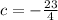
Hence, the equation of the perpendicular line is
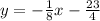
The equation of the parallel line is
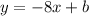
We find b using the point (-6, -5). Putting tn x = -6 and y = -5 gives
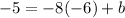
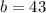
Hence, the equation of the parallel line is