we have the expressions
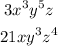
so
The GCF =(3)(x)(y^3)(z)
therefore
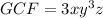
Remember that
The GCF is the largest positive integer that divides evenly into all numbers with zero remainder
so
To find out the GCF between two expressions, find out the prime factors
so
3x^3y^5z=(3)(x)(x)(x)(y)(y)(y)(y)(y)(z)
21xy^3z^4=(3)(7)(x)(y)(y)(y)(z)(z)(z)(z)
Select common factors with the smaller exponent
so
(3)(x)(y)(y)(y)(z)
GCF=3xy^3z