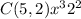Remember that according to the binomial theorem, the expression that gives the expansion of a binomial (a+b) raised to the nth power is:
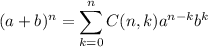
The first term can be obtained plugging in k=0, the second term by plugging in k=1 and the third term by plugging in k=2. Then, the third term of (x+2)^5 is given by the expression that results after setting n=5, k=2, a=x and b=2:
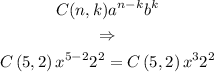
Therefore, the correct choice is: