First let's calculate the area of ABCD.
Using AD as the base, the height can be calculated with the difference of y-coordinates of the points B and A, and the base is the difference of x-coordinates of the points D and A:

So the area of ABCD is:
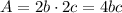
Now, finding the coordinates of the midpoints E, F, G and H, we have:
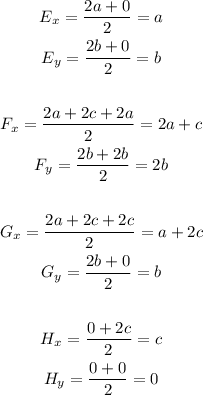
Using EG as a base of the triangles EGF and EGH, we can calculate the areas of these triangles.
The height of these triangles are the difference in y-coordinates of the point F and E:
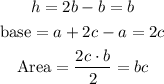
Adding the area of the two triangles, we have the area of EFGH:
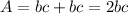
So comparing the area of EFGH and ABCD, we have:
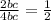
Therefore the area of EFGH is half the area of ABCD.