Answer:
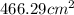
Step-by-step explanation: We have to find the surface area of the cylinder, the formula used is as follows:
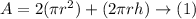
The height of the cylinder is:
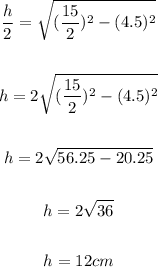
Therefore the surface area is calculated using the formula (1) as follows:
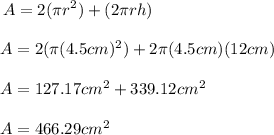
The surface area of the cylinder is 466.29 square centimeters.