Question

I need help solving this question, i don't understand it. Its related to compound interest

Answer 1

The rule of the compounded interest is

`A=P(1+(r)/(n))^(nt)`

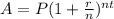
P is the initial amount

r is the ratio in decimal

n is the number of the periods in a year

t is the time in years

Since she will invest $75,000 for 4 years at 10.5% compounded annually, then

`\begin{gathered} P=75000 \\ r=(10.5)/(100)=0.105 \\ n=1 \\ t=4 \end{gathered}`

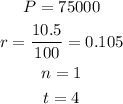
Substitute them in the rule above

`\begin{gathered} A=75000(1+(0.105)/(1))^(1(4)) \\ A=75000(1.105)^4 \\ A=111817.6538\text{ dollars} \end{gathered}`

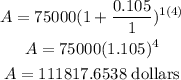
We will add it to the amount she pays now to find the total amount she must pay

`\begin{gathered} T=25000+11817.6538 \\ T=\text{ \$136817.6538} \end{gathered}`

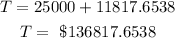
She needs now $136,817.6538