0. 3.5 years (approximately)
,
1. 78,125 female turtles.
1) SInce the equation that models this situation, the population of female turtles is:
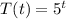
2) Then we can calculate that population in 7 years, by plugging t =7 and considering that the initial value is 5 then we can write when there will be 300 turtles:
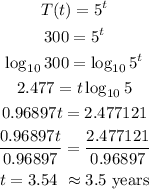
• Note that we had to use the properties of a logarithm to find that out.
,
• Rounding off to the nearest tenth, then approximately within 3.5 years there will be 300 turtles up there.
b) To find out how many female turtles will there be in 7 years?
We'll plug into that function t =7

Hence, we'll have 78, 125 female turtles.