Question

A bacteria culture is started with 300 bacteria. After 4 hours, the population had grown to 500 bacteria. If the population grows exponentially, determine the hourly growth rate of bacteria population

Answer 1

We will use the growth rate formula shown below:

`F=P(1+r)^n`

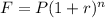
Where

F is the future amount

P is the initial amount

r is the rate of growth

n is the number of years

Given,

P = 300

F = 500 [after 4 years]

n = 4

We will have to find r. Substituting, we get:

`\begin{gathered} F=P(1+r)^n \\ 500=300(1+r)^4 \\ (500)/(300)=(300(1+r)^4)/(300) \\ (5)/(3)=(1+r)^4 \\ 1+r=\sqrt[4]{(5)/(3)} \\ r=\sqrt[4]{(5)/(3)}-1 \\ r=0.1367 \end{gathered}`

The growth rate is r = 0.14 [rounded]

In percent, it is:

0.14 * 100 = 14%

Hourly Growth Rate of Bacteria = 14%