ANSWER
• A = 55.5°
,
• B = 45.5°
,
• C = 79.1°
Step-by-step explanation
The lengths of the three sides of a triangle are given. We have to use the Law of Cosines to find the measures of the interior angles,
Solving each of the equations above for the angles, A, B, and C, we can find their measures,
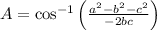
Replace the known values and solve,
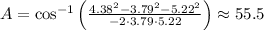
Repeat for angle B,
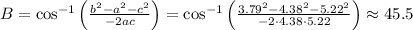
And for angle C,
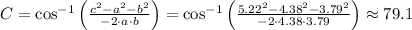
Hence, the three interior angles of this triangle, rounded to the nearest tenth of a degree, are:
• A = 55.5°
,
• B = 45.5°
,
• C = 79.1°