Question

Hi, can you help me with this question, please, thank you:)

Answer 1

Given:

The probability of growing oif healthy plant is p = 0.65 (65%).

The number of trials is n = 7.

Step-by-step explanation:

The probability for plant does not grow is,

`\begin{gathered} q=1-0.65 \\ =0.35 \end{gathered}`

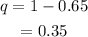
Probability for exactly 1 plant doesn't grow also means that 6 plants grow healthy.

The formula of binomial probability is,

`^nC_xp^xq^(n-x)`

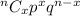
The value of x for this case is 6.

Substitute the values in the formula to detemine the probabilit for 6 plant grow healthy or 1 plant doesn't grow.

`\begin{gathered} ^7C_6(0.65)^6(0.35)^1=(7!)/(6!\cdot1!)\cdot(0.07541889)\cdot(0.35) \\ =0.18477 \\ \approx0.1848 \end{gathered}`

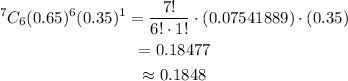
Answer: 0.1848