The statement "the length is 9 inches shorter than twice the width" can be expressed as
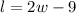
We know the height is 4 inches long, and the volume is 1,064 cubic inches.
The volume of a rectangular box is

Where w is x. Let's replace each given information.
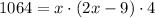
Now, we solve for x.
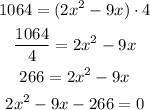
Where a = 2, b = -9, and c = -266. We use the quadratic formula to find the solutions.
![\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{-(-9)\pm\sqrt[]{(-9)^2-4(2)(-266)}}{2(2)} \\ x_(1,2)=\frac{9\pm\sqrt[]{81+2128}}{4}=\frac{9\pm\sqrt[]{2209}}{4}=(9\pm47)/(4) \\ x_1=(9+47)/(4)=(56)/(4)=14 \\ x_2=(9-47)/(4)=(-38)/(4)=-9.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ie5skqmayjoaabh5m7lym2r6hfyjwbmi17.png)
However, the positive number is the only one that makes sense to the problem since distances can't be negative.
Therefore, the right answer is 14 inches.