Question

Find x.Explain how to find x using trigonometryExplain how to find y using special right triangles.

Answer 1

Step 1: Write out the formula and the special triangle

`\sin \theta=(opp)/(hyp)`
`\begin{gathered} \text{Where} \\ \theta=\text{ an acute angle in a right-angled triangle} \\ \text{opp = the length of the side of the right-angled triangle opposite but not adjacent to }\theta \\ \text{hyp = the length of the hypotenuse of the right-angled triangle} \end{gathered}`

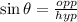
Step 2 (a): Write out the given values and substitute them into the formula

`\theta=30^0,hyp=24,opp=x`

Therefore,

`\begin{gathered} \sin 30^0=(x)/(24) \\ \text{this implies that} \\ (1)/(2)=(x)/(24) \\ \text{ Cross-multiplying, we have} \\ 2x=24 \\ \text{ Dividing both sides by 2, we have} \\ (2x)/(2)=(24)/(2) \\ x=12 \end{gathered}`

Step 2(b) Note that for the special triangle in Figure 1

The adjacent of angle 30 degrees is equal √3(the opposite of angle 30 degrees)

Therefore,

`y=\sqrt[]{3}x`