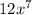Question

Given x > 0 rewrite the following expression in simplest form. 8

Answer 1

Firstly, we can separate the factors with the variable x and the factors without it.

When we have a multiplication inside a root, we can separate them into two roots:

`\sqrt[]{36x^8}\cdot\sqrt[4]{16x^(12)}=\sqrt[]{36}\sqrt[]{x^8}\cdot\sqrt[4]{16}\sqrt[4]{x^(12)}=\sqrt[]{36}\sqrt[4]{16}\cdot\sqrt[]{x^8}\sqrt[4]{x^(12)}`

For the factors without x, we can see that 36 is the same as 6 times 6 and 16 is the same as 2 * 2 * 2 * 2:

`\sqrt[]{36}\sqrt[4]{16}\cdot\sqrt[]{x^8}\sqrt[4]{x^(12)}=\sqrt[]{6^2}\sqrt[4]{2^4}\cdot\sqrt[]{x^8}\sqrt[4]{x^(12)}`

Now, we can apply the following property for all roots:

`\sqrt[c]{b^a}=b^{(a)/(c)}`

So, we have:

`\sqrt[]{6^2}\sqrt[4]{2^4}\cdot\sqrt[]{x^8}\sqrt[4]{x^(12)}=6^{(2)/(2)}2^{(4)/(4)}\cdot x^{(8)/(2)}x^{(12)/(4)}=6\cdot2\cdot x^4x^3=12\cdot x^4x^3`

Now, we can use the property:

`b^ab^c=b^(a+c)`

So:

`12x^4x^3=12x^(4+3)=12x^7`

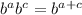
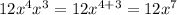
So, the simplest form is:

`12x^7`