Question

Jenny has a deck of 52 alphabet cards (26 uppercase and 26 lower case). Jenny selects one card. What is the probability that she selects a vowel, if on the first draw Jenny selects a vowel and does not replace it, how many cards remain, and how many are vowels. If she selected a vowel on her first draw without replacement, what is the probability she selects a vowel on her second draw?

Answer 1

There are 5 vowels and 10 of them with a vowel (5 uppercase and 5 lower case).

Now, we know that Jenny selected a vowel on her first draw, so there are 51 cards and 9 of them are vowel. Therefore, the probability that Jenny selects a vowel in a second draw is given by

`P(\text{ Jenny selects a vowel in the 2nd draw) =}(9)/(51)=0.1764`

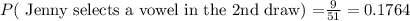
and there are 50 cards and 8 of them are vowels

On the other hand, if Jenny selected a vowel on her first draw but she replace the card, there are 52 cards again (10 of them are vowels). So, the probability that Jenny slects a vowel in the second draw is given by

`P(\text{ Jenny selects a vowel in the 2nd draw) =}(10)/(52)=0.1923`

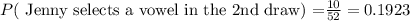
because the total number of cards doesn't change.

In summary, the answers are:

What is the probability that she selects a vowel, if on the first draw Jenny selects a vowel and does not replace it? Answer:

`(9)/(51)=0.18`

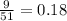
How many cards remain, and how many are vowels? Answer: It remains 50 cards and 8 of them are vowels.

If she selected a vowel on her first draw without replacement, What is the probability she selects a vowel on her second draw?​ Answer:

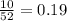
`(10)/(52)=0.19`

(