Function transformation rule
f(bx) horizontally stretches f(x) when 0 < |b| < 1. The point (x, y) is transformed into (x/b, y)
In this case, the transformation is:
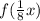
Considering the above rule:
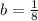
which satisfy the criterium:
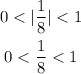
The point (x,y) in f(x) is transformed in f(x/8) as follows:
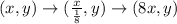
In conclusion, the graph of y = f(x/8) is obtained by a horizontal stretch of the graph of y = f(x) by multiplying each of its x-coordinates by 8