Question

someone drop 2 watermelons off a skyscraper the second watermelon is released 1s after the first water melon will the vertical distance always be the same this is yes it will always be BUT what will the Difference in velocity between the melons be after 4s of free fall

Answer 1

Take into account that the velocity for both watermelons can be written as follow:

`\begin{gathered} v=gt \\ v^(\prime)=gt^(\prime) \end{gathered}`

Consider that t' = t - 1, that is, second melon is released 1s after realted to the first one. Then:

`v^(\prime)=g(t-1)`

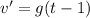
Where g is the acceleration gravitational constant.

If you calculate the difference v - v', you obtain:

`v-v^(\prime)=gt-g(t-1)=gt-gt+g=g`

As you can notice, the difference between the velocities is g, and this is a constant.

Hence, you can conclude that the difference in velocity between melons is constant and has a value of 9.8 m/s^2