ANSWERS
(a) 15000 J = 15 kJ
(b) 12.5 W
Step-by-step explanation
Given:
• Troy's mass, m = 60 kg
,
• The vertical distance his body is displaced, h = 25 m
,
• The time it takes him to reach the top of the hill, t = 20 minutes
Find:
• (a), The work he does running up the hill, W
,
• (b), Troy's power, P
(a) The work needed to climb the hill is equivalent to the potential energy Troy will have when he reaches the top of the hill, neglecting air resistance. Remember that work is the product between force and the distance the force is applied for, so we have,
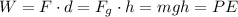
Replace the known values and solve,
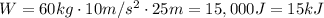
Hence, the work Troy does running up the hill is 15000 J (or 15 kJ).
(b) Power is the quotient between work and time,
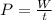
In this case, the time is given in minutes so, first, we have to convert it to seconds,
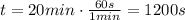
So the power is,
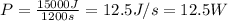
Hence, Troy's power is 12.5 W.