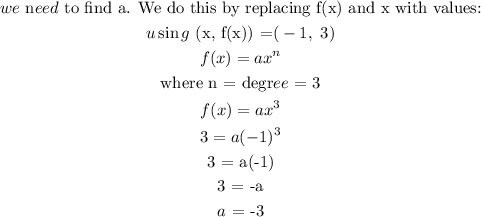Step-by-step explanation:
a) To determine the end behaviour, we need to sketch the points look on a graph:
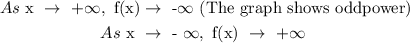
b) To determine the degree of the polynomial:
We find the difference in f(x) till we get a constant
difference 1: -23-(-4), -4-(3), 3-4, 4 - 5, 5 - 12, 12 - 31
= -19, -7, -1, -1, -7, -19
difference 2: -19-(-7), -7-(-1), -1(-1), -1-(-7), -7-(-19)
= -12, -6, 0, 6, 12
difference 3: -12-(-6), -6-0, 0-6, 6-12
= -6, -6, -6, -6
The constant is seen at the third difference. This is a cubic function
This means degree of the polynomial is 3.
Polynomial is cubic
c) Function in the form f(x) = ax^n