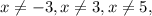Question

I need to find the answer in factored form and restrictions on the variable

Answer 1

Option A

`\begin{gathered} \frac{-2x(2x^{}+15)}{(x^{}-5)(x^{}-3)(x+3)} \\ x\\eq-3,3,5 \end{gathered}`

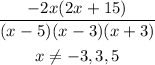
Step-by-step explanation:

Given the expression:

`(3x)/(x^2-2x-15)-(7x)/(x^2-8x+15)`

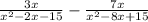
First, factorize each quadratic expression.

`\begin{gathered} =(3x)/(x^2-5x+3x-15)-(7x)/(x^2-3x-5x+15) \\ =\frac{3x}{x(x^{}-5)+3(x-5)}-\frac{7x}{x(x^{}-3)-5(x-3)} \\ =\frac{3x}{(x^{}-5)(x+3)}-\frac{7x}{(x^{}-3)(x-5)} \end{gathered}`

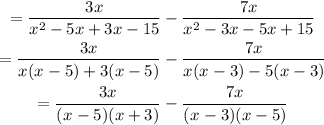
Next, find the lowest common multiple of the denominators:

`=\frac{3x(x-3)-7x(x+3)}{(x^{}-5)(x^{}-3)(x+3)}`

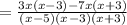
Open the bracket in the numerator and simplify:

`\begin{gathered} =\frac{3x^2-9x-7x^2-21x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{3x^2-7x^2-9x-21x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{-4x^2-30x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{-2x(2x^{}+15)}{(x^{}-5)(x^{}-3)(x+3)} \end{gathered}`

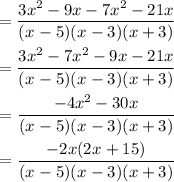
The restrictions on the variable are:

`x\\e-3,x\\e3,x\\e5,`