Step-by-step explanation
In the equation, we can see that the lateral sides of the frustum are made up of trapezium.
We can extrapolate a part below.
We can find the lateral surface area using the formula below;

Answer 1: 124.8 square foot
To find the volume of the frustum we will use the formula below;
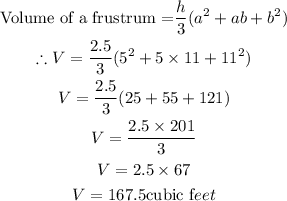
Answer 2: 167.5 cubic feet