Looking at the figure, we can determine the following relations:
A.
The angles ∠BFC and ∠DFE are vertical angles.
B.
The angles ∠BFA and ∠DFE are neither vertical angles or a linear pair.
C.
The angles ∠BFC and ∠CFD are a linear pair.
D.
The angles ∠AFE and ∠AFC are a linear pair.
E.
The angles ∠BFE and ∠CFD are vertical angles.
F.
The angles ∠AFE and ∠BFC are neither vertical angles or a linear pair.
Since the angle ∠EFD is 50° and the angles ∠AFB and ∠EFD are congruent, the angle ∠AFE can be found with the relation:
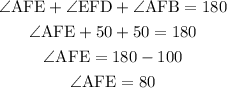
The angles ∠DFC and ∠BFE are vertical angles, so we have:
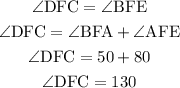
The angles ∠BFC and ∠EFD are vertical angles, so they are congruent, therefore we have ∠BFC = 50°.