Answer:
44 square mm
Step-by-step explanation:
The surface area of the triangular pyramid is the sum of the surface areas of the 4 triangles.
Since the base is an equilateral triangle, the surface area:
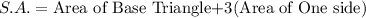
Base Area
![A=(1)/(2)bh=(1)/(2)*4*1=2\operatorname{mm}^2]()
Area of one side
![A=(1)/(2)bh=(1)/(2)*4*7=14\operatorname{mm}^2]()
Thus, the surface area is:
![\begin{gathered} S\mathrm{}A\mathrm{}=2+3(14) \\ =2+42 \\ =44\operatorname{mm}^2 \end{gathered}]()
The surface area is 44 square mm.